William H. Calvin University of Washington Box 351800 Seattle WA 98195-1800 USA Email || Home Page || publication list |
as it appeared in copyright ©1975 by authors and publisher. |
William H. Calvin University of Washington Box 351800 Seattle WA 98195-1800 USA Email || Home Page || publication list |
as it appeared in copyright ©1975 by authors and publisher. |
Brain Research, 84 (1975)1-22 ~ Elsevier Scientific Publishing Company, Amsterdam -Printed in The NetherlandsReview Article
GENERATION OF SPIKE TRAINS IN CNS NEURONS
WILLIAM H. CALVIN
Department Neurological Surgery, University of Washington School of Medicine, Seattle, Wash. 98195 (U.S.A.)
(Accepted October 4th, 1974)
SUMMARYThe membrane potential waveforms to be expected from many asynchronous inputs to CNS neurons are described, along with three modes for repetitive firing through which the input waveforms are converted into spike trains. Area beneath a postsynaptic potential (PSP), rather than PSP peak height, is shown to be an important parameter susceptible to modification.
Occasional crossings of threshold produce occasional spikes, but a sustained depolarizing waveform which attempts to hold the membrane potential above threshold elicits rhythmic firing. Firing rate is graded with the amount by which the synaptic depolarizing currents exceed the minimum current for rhythmic firing (approximately rheobase). A systematic sequence of alterations in the membrane potential trajectory between spikes, quite different from those of receptors and invertebrate neurons, may control the firing rate and give rise to sudden changes in the 'gain' of this conversion of depolarizing current into firing rate. The different implications of synaptic location during the occasional spike mode and the rhythmic firing mode are discussed, as is the role of the antidromic invasion of the soma-dendritic region during rhythmic firing.
Less frequently, an 'extra spike mode' is seen where depolarizing afterpotentials following a spike themselves cross threshold to elicit an extra spike, which may similarly elicit another extra spike, etc., in a regenerative cycle. The character of the underlying depolarizing afterpotentials (or 'delayed depolarizations') is reviewed, along with theories for their origin from the antidromic invasion of the dendritic tree.
The stereotyped burst firing patterns characteristic of the extra spike mode can also be seen in deafferented neurons and neurons studied in chronic syndromes such as epilepsy and central pain. This raises the question as to whether some disease states may augment extra spike firing, thus multiplying many-fold the response to a normal input.INTRODUCTION
The most obvious electrical property of a nerve cell is its threshold. If there is insufficient input, there will be no output. The inputs take the form of transient membrane potential changes called postsynaptic potentials (PSPs); the output is usually in the form of action potentials (or 'spikes') which propagate down the axon to eventually generate PSPs in the next cell. The individual inputs are usually not very potent in the central nervous system (CNS), unlike obligatory synapses such as neuromuscular junctions: an individual afferent fiber or interneuron often produces a PSP in the next cell which is smaller than 2% of the voltage change needed to reach thresholds 56 58,62,63,70. While experimenters often synchronize many inputs to produce a large compound PSP (Fig. 1E) which can cross threshold93, this artificial situation provides little physiological insight into how temporal patterns of inputs produce trains of output spikes. This article attempts to elucidate (1) the depolarization waveform to be expected from the summation of many asynchronous input PSP trains, and (2) 3 different modes of repetitive firing (Fig. 1A, B and D) through which input waveforms are transformed into output spike trains. Variations in firing pattern due to cell properties will be emphasized, e.g., rhythmic firing due to membrane properties, but not those due to periodic inputs. Some of the abnormal neuron spike trains in pathological pain and epilepsy will then be examined.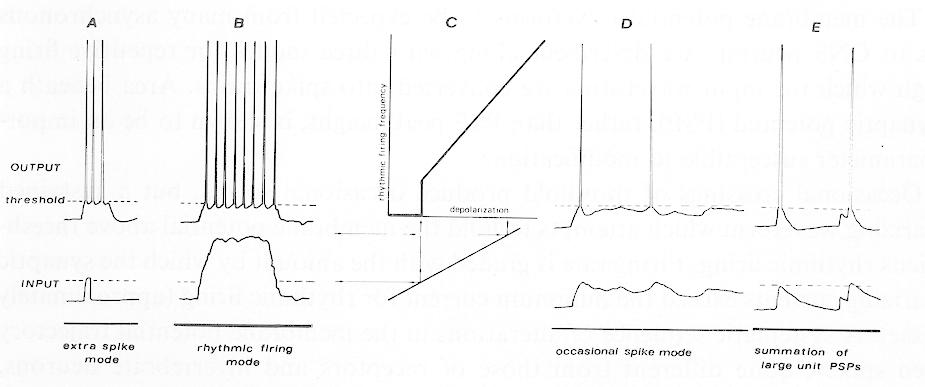 Fig. 1. Schematic drawings of repetitive firing. Lower traces (input) represent membrane potential which would be seen if spike generation were artificially prevented. Upper traces (output) shows spike train generation by these input waveforms. A: regenerative firing mode, where large depolarizing afterpotentials rise through the falling threshold after a spike to set off an extra spike, which may itself set off another extra spike, etc. This firing may outlast the original depolarizing stimulus 39. B: rhythmic firing mode, caused by the interaction of the spike's hyperpolarizing afterpotential with the sustained input currents. C: once it exceeds threshold, further increases in the depolarizing current cause linear increments in firing rate. D: input waveforms which only occasionally exceed threshold (at times long compared to the afterpotential durations) cause occasional spikes. E: case where single PSPs are large, individually or cooperatively eliciting spikes. Also illustrative of the artificial situation normally used in most neurophysiological experiments, where many small inputs are artificially synchronized by an electric shock to produce a large compound excitatory postsynaptic potential (EPSP). While the last situation is the usual view of how inputs cooperate to produce spikes, it is an unrepresentative one because most single inputs are very small (less than 2% of the threshold voltage change) and seldom synchronized. Thus, input waveforms such as seen in B and D are more representative than E. See text.Summation of input PSPs
Fig. 1. Schematic drawings of repetitive firing. Lower traces (input) represent membrane potential which would be seen if spike generation were artificially prevented. Upper traces (output) shows spike train generation by these input waveforms. A: regenerative firing mode, where large depolarizing afterpotentials rise through the falling threshold after a spike to set off an extra spike, which may itself set off another extra spike, etc. This firing may outlast the original depolarizing stimulus 39. B: rhythmic firing mode, caused by the interaction of the spike's hyperpolarizing afterpotential with the sustained input currents. C: once it exceeds threshold, further increases in the depolarizing current cause linear increments in firing rate. D: input waveforms which only occasionally exceed threshold (at times long compared to the afterpotential durations) cause occasional spikes. E: case where single PSPs are large, individually or cooperatively eliciting spikes. Also illustrative of the artificial situation normally used in most neurophysiological experiments, where many small inputs are artificially synchronized by an electric shock to produce a large compound excitatory postsynaptic potential (EPSP). While the last situation is the usual view of how inputs cooperate to produce spikes, it is an unrepresentative one because most single inputs are very small (less than 2% of the threshold voltage change) and seldom synchronized. Thus, input waveforms such as seen in B and D are more representative than E. See text.Summation of input PSPs
If one stretches a muscle, the asynchronous discharge of many receptors (and subsequently interneurons) produces a barrage of PSPs in CNS neurons. In these downstream neurons, a sustained depolarization (or hyperpolarization) develops with a ripple atop it reflecting the arrival of the individual PSPs. The average depolarization shift depends upon the size of each input (actually, the area beneath the PSP), its rate, and its polarity12. Excitatory PSPs (EPSPs) are depolarizing while inhibitory PSPs (IPSPs) tend to hyperpolarize the cell membrane away from threshold. We will consider one input at a time to see how the temporal summation process effectively converts an input rate into an average depolarization level.
Fig. 2 shows the way in which PSPs temporally summate until a plateau is reached where the voltage decays as much after a PSP as it rises upon the next PSP. The mean height of this plateau is proportional to the rate of the PSPsl2, as shown in the graph. If the individual PSPs are smaller, the proportionality constant between plateau level and PSP rate is less: this slope is the area beneath a single PSP. The 'PSPs' illustrated are simulated PSPsl2 and assume linear summation of PSPs; the differences between real PSPs and linear theory will be discussed presently.
The PSP arrival rates illustrated for temporal summation are rather high; what if PSPs come along more slowly? As seen for 6 inputs with low rates in Fig. 2, a PSP can decay almost to the baseline before another PSP comes along, i.e., no plateau develops. If one averages the membrane potential over a 1-see period, however, it will be found to accord with the prediction made by multiplying the average PSP arrival rate by the area beneath a single PSP. One may argue that the neuron does not 'see' the average membrane potential, but rather the instantaneous membrane potential. However, the neuron really does not see the individual PSP peak either (because most PSPs are miniscule, e.g., less than 1-2% of the subthreshold swing of the membrane potential).
When many inputs are active and superimpose their PSP trains, one sees enough 'spatial' summation to produce steady depolarizations ('spatial' summation is a classical neurophysiological term for what mathematicians call superposition; it need not have geometric implications). Fig. 2 shows 6 inputs firing at low rates, rhythmically but asynchronously; the resulting superposition is shown below. The mean level in spatial summation is merely the sum of the calculated mean depolarizations for each of the 6 inputs. Of course, the arrivals in spatial summation appear irregular and the voltage wanders around randomlyl7. The essential features are exactly what one records in a motoneuron upon stretching a muscle (a baseline shift and noise).
The same linear theory applies to the summation in the muscle tendons of the twitch tensions of the individual motor units. Imagine that the ordinate in Fig. 2 is tension rather than membrane potential. The 6 inputs are now 6 different motor units, due to 6 motoneurons firing asynchronously; the spatial summation in Fig. 2 shows the muscle tension to be expected if different motor units summate linearly with one another, i.e., if the plot of average tension vs. rates is a straight line, as in Fig. 2. Of course, they may summate nonlinearly for a variety of reasons; indeed, Rack and Westbury78 have shown that the actual curve is S-shaped. Similarly, for the membrane potential case, facilitation will make individual PSPs bigger at high rates 67 74; however, large plateau depolarizations will reduce the distance to the PSP reversal potential, and thus decrease the individual PSP size68. Just how much these opposing factors will deviate the depolarization vs. rate curve from a straight line will have to be evaluated in each case. For example, one expects 1A afferent inputs to motoneurons57 to behave more linearly than corticospinal inputs74 because of differences in facilitation. The basic relation, however, is average plateau equals rate multiplied by the area beneath the typical unitary response. This plateau in a CNS neuron is analogous to the receptor potential of peripheral receptor neurons.SCAN TO BE CONTINUED....
Fig. 2. Temporal and spatial summation of inputs, using computer simulations of linear summation. The input rate is doubled and tripled to show higher plateau depolarizations developing in temporal summation. Graph at right shows linear relation between PSP rate and average depolarization developed; the slope of this curve is merely the area beneath a single PSP (inset). When input rates are slower (middle), a plateau is not obvious but the average depolarization over I sec is still predicted by the graph. When one sums together the activity in 6 inputs (all firing rhythmically but asynchronously), the resulting sum (bottom) shows a plateau depolarization which can be predicted from the sum of the area x rate products of the 6 individual inputs. The ripple about the plateau corresponds to what is called 'synaptic noise' in CNS neurons12'l7. Adapted from Calvin12.